指定駅まで所要時間の採集

東京都内までの通勤の苦労を控えるため、便利な場所を見つけるスクリプトです。

まず、このサイト（https://ensenmin.com/first）による候補者を取ります。

候補者の中に重複の駅名をまず取り出します。

そして、Pythonのseleniumモジュールを利用し、ブラザーの行動を模擬します。
Yahoo乗換案内(https://transit.yahoo.co.jp/)のソースを見ながら、regexで情報を特定します。
取り出したい情報は始発駅、始発時間、到着時間、乗り換え数です。
時間コストはTimestampで差を計算し、Strに変更してDataFrameに次々と更新します。
最後にExcelで出力します。

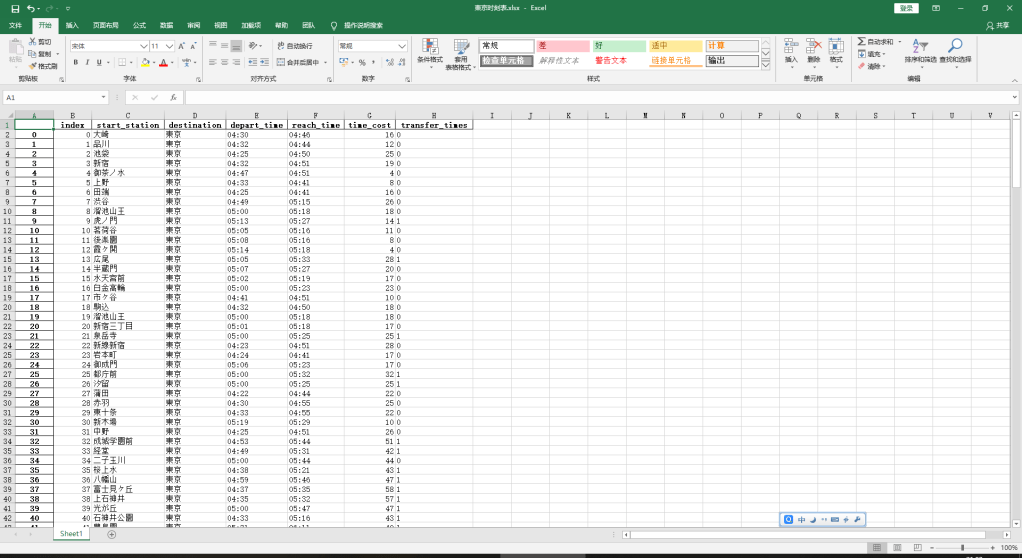
そして、新宿駅までの経由も調べて、並べれば、下記のようです。

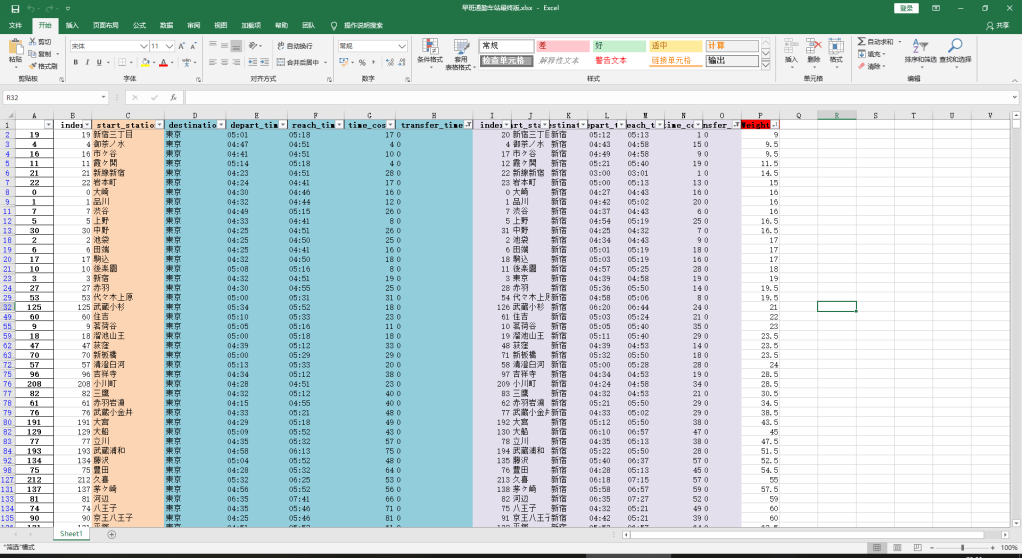
家賃も考えて、住みたいところは選べると思います。

コードは下記です。

# -*- coding: utf-8 -*
import urllib.request
import random
from urllib.request import urlopen
from bs4 import BeautifulSoup
import re
import math
import time
import datetime
import pandas as pd
import numpy as np
import requests
from selenium import webdriver
from selenium.webdriver.chrome.options import Options

STATION_RECOMMENDATION_LINK = 'https://ensenmin.com/first'  #
INFORMATION_DIC = {}
INFORMATION_DF = pd.DataFrame({'index': [], 'start_station': [], 'destination': [],
                               'depart_time': [], 'reach_time': [], 'time_cost': [], 'transfer_times': []}, index=None)
STATION_CANDIDATES = []
yahoo_link = 'https://transit.yahoo.co.jp/'


def look_up_route(depart_station, destination, index):
    chrome_driver = webdriver.Chrome(r'C:\Users\cdkag\Desktop\租房爬虫\chromedriver.exe')
    chrome_driver.get(yahoo_link)
    chrome_driver.find_element_by_id('sfrom').send_keys(depart_station)
    chrome_driver.find_element_by_id('sto').send_keys(destination)  # 到达站选择
    chrome_driver.find_element_by_id('air').click()
    chrome_driver.find_element_by_id('sexp').click()
    chrome_driver.find_element_by_id('exp').click()
    chrome_driver.find_element_by_id('hbus').click()
    chrome_driver.find_element_by_id('bus').click()
    chrome_driver.find_element_by_id('fer').click()  # 排除渡轮
    chrome_driver.find_element_by_id('tsFir').click()  # 始发选择
    chrome_driver.find_element_by_id('y').send_keys('2020')  # 时刻表年份
    chrome_driver.find_element_by_id('m').send_keys('3')  # 时刻表月份
    chrome_driver.find_element_by_id('d').send_keys('2')  # 时刻表天数
    chrome_driver.find_element_by_id('hh').send_keys('6')  # 时刻表小时
    chrome_driver.find_element_by_id('mm').send_keys('0')  # 时刻表分钟
    chrome_driver.find_element_by_class_name('optSort').find_element_by_tag_name('select').send_keys('乗り換え回数順')
    element = chrome_driver.find_element_by_id('searchModuleSubmit')  # 定位提交按钮
    element.submit()  # 提交页面
    # print('current_url:\n', chrome_driver.current_url)  # 读取当前页面地址
    new_page = BeautifulSoup(urlopen(chrome_driver.current_url).read(), 'html.parser')
    start_time_bs = new_page.find_all('li', {'class': 'time'})[1].get_text()
    depart_time = re.search(r'(\d){2}(\:)(\d){2}', start_time_bs).group()
    print('出发时间： ', depart_time)
    reach_time = new_page.find_all('li', {'class': 'time'})[1].get_text()
    reach_time = re.search(r'(\→)(\d){2}(\:)(\d){2}', reach_time).group()[1:]
    # reach_time = new_page.find_all('li', {'class': 'time'})[1].find('span', {'class': 'mark'}).get_text()
    print('到达时间： ', reach_time)
    start_time_cal = datetime.datetime.strptime(depart_time, '%H:%M')  # 获取最新日期表示为时间戳类型
    reach_time_cal = datetime.datetime.strptime(reach_time, '%H:%M')  # 获取最新日期表示为时间戳类型
    time_cost = str(re.search(r'(\d){1}(\:)(\d){2}', str(reach_time_cal - start_time_cal)).group())
    print(int(time_cost[:1]), int(time_cost[2:]))
    time_cost = int(time_cost[:1]) * 60 + int(time_cost[2:])
    print('耗时： ', time_cost, ' mins')
    transfer_times = re.search(r'(\d)+', new_page.find_all('li', {'class': 'transfer'})[0].find('span', {
        'class': 'mark'}).get_text()).group()
    print('换乘次数： ', transfer_times)
    INFORMATION_DF.loc[index] = [index, depart_station, destination,
                                 depart_time, reach_time, time_cost, transfer_times]
    INFORMATION_DF.to_excel('Yahoo时刻表.xlsx')
    chrome_driver.close()


if __name__ == '__main__':
    dic_candi = ['大崎', '品川', '池袋', '東京', '新宿', '御茶ノ水', '上野', '田端', '渋谷', '虎ノ門', '茗荷谷', '後楽園', '霞ヶ関', '広尾', '半蔵門', '水天宮前', '白金高輪', '市ヶ谷', '駒込', '溜池山王', '新宿三丁目', '泉岳寺', '新線新宿', '岩本町', '御成門', '都庁前', '汐留', '蒲田', '赤羽', '東十条', '新木場', '中野', '成城学園前', '経堂', '二子玉川', '桜上水', '八幡山', '富士見ヶ丘', '上石神井', '光が丘', '石神井公園', '豊島園', '成増', '上板橋', '竹ノ塚', '青砥', '高砂', '浅草', '荻窪', '中野富士見町', '中目黒', '北千住', '南千住', '八丁堀', '代々木上原', '綾瀬', '北綾瀬', '押上', '清澄白河', '東陽町', '京急蒲田', '住吉', '赤羽岩淵', '王子神谷', '小竹向原', '西馬込', '浅草橋', '大島', '笹塚', '西高島平', '高島平', '新板橋', '新御徒町', '東京テレポート', '高尾', '八王子', '豊田', '武蔵小金井', '立川', '青梅', '武蔵五日市', '奥多摩', '河辺', '三鷹', '町田', '稲城長沼', '西国立', '府中本町', '唐木田', '多摩センター', '高尾山口', '京王八王子', '高幡不動', '若葉台', 'つつじヶ丘', '府中', '北野', '吉祥寺', '清瀬', '保谷', '拝島', '玉川上水', '西武遊園地', '磯子', '鶴見', '東神奈川', '桜木町', '小机', '中山', '矢向', '長津田', '菊名', '横浜', '元町・中華街', '日吉', '金沢文庫', '神奈川新町', '川崎', '京急川崎', '登戸', '武蔵中原', '武蔵溝ノ口', '溝の口', '向ヶ丘遊園', '新百合ヶ丘', '鷺沼', '武蔵小杉', '元住吉', '久里浜', '逗子', '大船', '横須賀', '平塚', '小田原', '国府津', '藤沢', '二宮', '橋本', '茅ヶ崎', '本厚木', '新松田', '秦野', '伊勢原', '海老名', '相模大野', '相武台前', '片瀬江ノ島', '中央林間', '三崎口', '浦賀', '新逗子', '三浦海岸', '堀ノ内', 'かしわ台', '大和', '二俣川', '千葉', '幕張', '蘇我', '海浜幕張', '千葉中央', '津田沼', '西船橋', '君津', '上総一ノ宮', '佐倉', '成東', '成田', '成田空港', '木更津', '我孫子', '松戸', '柏', '新習志野', '上総湊', '勝浦', '南船橋', '京成臼井', '京成佐倉', '京成成田', '京成大和田', '宗吾参道', '東成田', 'ちはら台', '芝山千代田', '印旛日本医大', '印西牧の原', '妙典', '浦安', '東葉勝田台', '八千代緑が丘', '本八幡', '大宮', '南浦和', '武蔵浦和', '指扇', '浦和美園', '川越市', '本川越', '南古谷', '高麗川', '籠原', '深谷', '東所沢', '南越谷', '飯能', '小手指', '所沢', '狭山市', '小川町', '森林公園', '志木', '上福岡', '久喜', '東武動物公園', '北越谷', '北春日部', '南栗橋', '八潮', '鳩ケ谷', '和光市', '鹿島神宮', '古河', '取手', '土浦', '勝田', '水戸', '高萩', 'つくば', '守谷', '宇都宮', '小金井', '黒磯', '氏家', '高崎', '新前橋', '前橋', '館林', '熱海', '伊東', '沼津', '大月', '河口湖']
    START_LOG = 0
    df = pd.read_html(STATION_RECOMMENDATION_LINK)
    for i in range(1, len(df[-1])):
        phrase = re.split('、', df[-1][1].iloc[i])
        for j in range(len(phrase)):
            STATION_CANDIDATES.append(phrase[j])
    print(len(STATION_CANDIDATES))
    print(STATION_CANDIDATES)
    dic_candi.remove('東京')
    for each in range(len(dic_candi)):
        look_up_route(dic_candi[each], '東京', START_LOG)
        START_LOG = 1 + START_LOG
        time.sleep(1)

用HOG特征进行固定尺寸的人脸识别

# -*- coding: UTF-8 -*-
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from skimage import data, color, feature
from sklearn.datasets import fetch_lfw_people
import skimage.data
from itertools import chain  # 用于组合样本
from skimage import data, transform
from sklearn.feature_extraction.image import PatchExtractor
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import cross_val_score
from sklearn.svm import LinearSVC
from sklearn.model_selection import GridSearchCV
sns.set()


def sliding_window(img, patch_size, istep=2, jstep=2, scale=1):  # 然而当要预测照片的尺寸和学习模型学习的尺寸不一样时候，效果打折
    print('patch_size:', patch_size)
    Ni, Nj = (int(scale * s) for s in patch_size)  # 找到缩略图像素框总长宽
    print('sliding_window_img.shape: ', img.shape)
    # print('Ni:', Ni)
    # print('Nj:', Nj)
    for i in range(0, img.shape[0] - Ni, istep):  # 长度方向步进2
        for j in range(0, img.shape[1] - Ni, jstep):  # 宽度方向步进2
            patch = img[i:i + Ni, j:j + Nj]  # 新缩略图大小被步进窗口赋值
            if scale != 1:  # 不是1的话，则化为patch_size大小
                patch = transform.resize(patch, patch_size)
            yield (i, j), patch  # 生成返回窗口坐标，HOG特征窗口对象


def extract_patches(img, N, patch_size, scale=1.0):  # N是每个尺寸照片的训练样本数，patch_size是用来显示的尺度
    print('img.shape:\n', img.shape)
    # print('img[np.newaxis].shape:\n', img[np.newaxis].shape)
    print('scale:\n', scale)
    print('patch_size):\n', patch_size)
    print('scale * np.array(patch_size):\n', scale * np.array(patch_size))  # 元组化为数组后扩大缩小尺寸
    extracted_patch_size = tuple((scale * np.array(patch_size)).astype(int))  # 对原图数据放大缩小后，numpy.float64化为元组，抽出尺寸化为整形
    print('extracted_patch_size:\n', extracted_patch_size)
    # PatchExtractor类支持多幅图像作为输入
    extractor = PatchExtractor(patch_size=extracted_patch_size, max_patches=N, random_state=0)  # 能按照不同size抽出的抽出器
    patches = extractor.transform(img[np.newaxis])  # img[np.newaxis]增加一个维度，eg: (872, 1000) -> (1, 872, 1000)，抽出转换
    # print('patches.shape:', patches.shape, 'scale:', scale)  # N*(img.shape转换为缩略图的维度)
    if scale != 1:
        # 尺寸需要被改变，变为patch_size
        patches = np.array([transform.resize(patch, patch_size) for patch in patches])  # 改变图片尺寸resize
    # print('patches.shape', patches.shape, 'scale:', scale)  # (N*patch_size)维
    return patches


image = color.rgb2gray(data.chelsea())  # color.rgb2gray(): RGB转为灰度图； data.chelsea()代表小猫切尔西
print('feature.hog(image, visualize=True):\n', feature.hog(image, visualize=True))  # 输入图像， visualize：是否输出HOG image梯度图
hog_vec, hog_vis = feature.hog(image, visualize=True)
fig, ax = plt.subplots(1, 2, figsize=(12, 6), subplot_kw=dict(xticks=[], yticks=[]))
ax[0].imshow(image, cmap='gray')
print('image.shape: ', image.shape)
ax[0].set_title('input image')
ax[1].imshow(hog_vis)
print('hog_vis.shape: ', hog_vis.shape)
ax[1].set_title('visualization of HOG features')

faces = fetch_lfw_people()
positive_patches = faces.images  # 获取含有人脸的图片作为正训练样本
print('positive_patches.shape:', positive_patches.shape)
imgs_to_use = ['camera', 'text', 'coins', 'moon', 'page', 'clock', 'immunohistochemistry', 'chelsea',
               'coffee', 'hubble_deep_field']
# 把这些主题的照片都转换成灰度图
# print('getattr(data, name)', getattr(data, imgs_to_use[0]))
images = [color.rgb2gray(getattr(data, name)()) for name in imgs_to_use]  # getattr(data, name)返回data对象的一个name属性，是函数对象
# 对所有负训练对象的图片做抽出缩略图操作，化为和正训练对象一样尺寸大小
# np.vstack()能去除冗余维度
negative_patches = np.vstack([extract_patches(im, 1000, positive_patches[0].shape, scale) for im in images for scale in [0.5, 1.0, 2.0]])
print('negative_patches.shape:', negative_patches.shape)

fig2, ax2 = plt.subplots(6, 10)
for i, axi in enumerate(ax2.flat):
    axi.imshow(negative_patches[500 * i], cmap='gray')
    axi.axis('off')

X_train = np.array([feature.hog(im) for im in chain(positive_patches, negative_patches)])  # 将正负样本组合，计算HOG特征
y_train = np.zeros(X_train.shape[0])  # 用0填充X_train样本数作为长度的数组
# print('X_train.shape:\n', X_train.shape)
# print('positive_patches.shape:\n', positive_patches.shape)
y_train[:positive_patches.shape[0]] = 1  # 设开始正样本结果为1
# print('X_train.shape: ', X_train.shape)
# cv的意思是验证5次结果
print('cross_val_score(GaussianNB(), X_train, y_train):', cross_val_score(GaussianNB(), X_train, y_train, cv=3))
grid = GridSearchCV(LinearSVC(), {'C': [0.0625, 0.125, 0.25, 0.5]}, cv=3)
grid.fit(X_train, y_train)
print('grid.best_score_: ', grid.best_score_)
print('grid.best_params_: ', grid.best_params_)
# 用最优参数得到最优评估器
model = grid.best_estimator_
model.fit(X_train, y_train)
model.fit(X_train, y_train)

fig3, ax3 = plt.subplots()
test_image = skimage.data.astronaut()  # 给一个航天员作为未知新图输入
test_image = skimage.color.rgb2gray(test_image)
test_image = skimage.transform.rescale(test_image, 0.5)  # 缩小到0.5倍
test_image = test_image[:160, 40:180]  # 改成适应学习的尺寸
plt.imshow(test_image, cmap='gray')
plt.axis('off')
print('test_image.shape:', test_image.shape)
indices, patches = zip(*sliding_window(test_image, positive_patches[0].shape))  # indices:赋值矩形左下角坐标，patches:方框们
patches_hog = np.array([feature.hog(patch) for patch in patches])  # 计算生成器产生的HOG特征
print('patches_hog.shape:', patches_hog.shape)

labels = model.predict(patches_hog)  # 预测有HOG特征的图
print('The total number of the pictures with human faces is: ', labels.sum())  # 这幅图能被确定到的人脸方框数量

fig4, ax4 = plt.subplots()
ax4.imshow(test_image, cmap='gray')
ax4.axis('off')

Ni, Nj = (positive_patches[0]).shape  # 高，宽
indices = np.array(indices)

for i, j in indices[labels == 1]:
    ax4.add_patch(plt.Rectangle((j, i), Nj, Ni, edgecolor='red', alpha=0.3, lw=2, facecolor='none'))
plt.show()

用KDE做贝叶斯生成分类

# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.neighbors import KernelDensity
from sklearn.datasets import load_digits
from sklearn.model_selection import GridSearchCV
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import cross_val_score


class KDEClassifier(BaseEstimator, ClassifierMixin):  # 基于KDE的贝叶斯生成分类
    # bandwidth是每个类中的核带宽(float);kernel是核函数名称
    def __init__(self, bandwidth=1.0, kernel='gaussian'):
        self.bandwidth = bandwidth
        self.kernel = kernel

    def fit(self, X, y):
        self.classes_ = np.sort(np.unique(y))  # np.unique():去除数组中的重复数字，并进行排序之后输出，小到大
        print('X:\n', X)
        print('y:\n', y)
        print('self.classes_:\n', self.classes_)
        # 在训练数据集中找到所有标签类，去掉重复标签
        training_sets = [X[y == yi] for yi in self.classes_]  # 按y里的元素从小到大的顺序遍历X的行数，行索引号由出现y里元素index号决定
        # 为每个类（各traning_set）训练一个KernelDensity模型
        self.models_ = [KernelDensity(bandwidth=self.bandwidth, kernel=self.kernel).fit(Xi) for Xi in training_sets]
        # 计算类的先验概率，某类标签yi时总计概率Xi/X
        self.logpriors_ = [np.log(Xi.shape[0] / X.shape[0]) for Xi in training_sets]
        return self

    # 预测新数据概率
    def predict_proba(self, X):
        # 得到每个类别的概率密度估计值形成的数组shape:[n_samples*n_classes]，这里数组中[i,j]表示样本i属于j类的后验概率
        logprobs = np.array([model.score_samples(X) for model in self.models_]).T  # 这里因为是矩阵，所以np.array和np.vstack都是一样效果
        # 数字0这个训练模型训练出来的概率密度，元素数量取决于带宽
        print('self.models_[0].score_samples(X).shape:\n', self.models_[0].score_samples(X).shape)
        # 模型不同预测所需要的n_samples的特征数组也不一样， 359可以是357等等，有的模型是预测0，有的模型是预测1
        print('logprobs.shape:\n', logprobs.shape)  # (359, 10)之类
        print('logprobs:\n', logprobs)
        # 各自取指数还原，然后乘以先验概率
        result = np.exp(logprobs + self.logpriors_)
        # 返回归一化后的result统一单位
        return result / result.sum(1, keepdims=True)

    def predict(self, X):
        # 返回拥有最大概率的类别
        print('self.classes_[np.argmax(self.predict_proba(X), 1)]:\n', self.classes_[np.argmax(self.predict_proba(X), 1)])
        return self.classes_[np.argmax(self.predict_proba(X), 1)]  # np.argmax():返回最大值索引, 0代表跨行查找最大（即列）, 1代表跨列查找最大（即行）


digits = load_digits()
print('digits.data.shape:\n', digits.data.shape)
bandwidths = 10 ** np.linspace(0, 2, 100)
grid = GridSearchCV(KDEClassifier(), {'bandwidth': bandwidths}, cv=5, iid=False)  # , cv=5, iid=False
grid.fit(digits.data, digits.target)

# print("grid.cv_results_['mean_test_score']:\n", grid.cv_results_['mean_test_score'])
scores = [val for val in grid.cv_results_['mean_test_score']]
plt.semilogx(bandwidths, scores)  # 把x轴用对数刻度显示
plt.xlabel('bandwidth')
plt.ylabel('accuracy')
plt.title('KDE Model Performance')
print(grid.best_params_)
print('\naccuracy =', grid.best_score_)
print('cross_val_score(GaussianNB(), digits.data, digits.target).mean(): ',
      cross_val_score(GaussianNB(), digits.data, digits.target, cv=5).mean())
plt.show()

物种分布密度的例子(球形空间KDE)

# -*- coding: UTF-8 -*-
from sklearn.datasets import fetch_species_distributions
from mpl_toolkits.basemap import Basemap
from sklearn.datasets.species_distributions import construct_grids
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity

data = fetch_species_distributions()
# 获取物种ID和位置矩阵、数组
latlon = np.vstack([data.train['dd lat'], data.train['dd long']]).T
print('latlon.shape: ', latlon.shape)
# .startswith('micro')检查字符串是否是以micro字符串开头, 返回布尔数组
species = np.array([d.decode('ascii').startswith('micro') for d in data.train['species']], dtype='int')
print('species.shape: ', species.shape)
xgrid, ygrid = construct_grids(data)  # 创建格子，供形成地理图的坐标用
m = Basemap(projection='cyl', resolution='c', llcrnrlat=ygrid.min(), urcrnrlat=ygrid.max(),
            llcrnrlon=xgrid.min(), urcrnrlon=xgrid.max())
m.drawmapboundary(fill_color='#DDEEFF')
m.fillcontinents(color='#FFEEDD')
m.drawcoastlines(color='gray', zorder=2)
m.drawcountries(color='gray', zorder=2)
m.scatter(latlon[:, 1], latlon[:, 0], zorder=3, c=species, cmap='rainbow', latlon=True)

# 用核密度估计对分布点进行概率分布（平滑化）
# 画轮廓图的数据点
X, Y = np.meshgrid(xgrid[::5], ygrid[::5][::-1])  # 每五个挑出（减小机器负担），ygrid最后还要倒序
# http://wiki.swarma.net/index.php?title=%E9%A2%84%E6%B5%8B%E7%89%A9%E7%A7%8D%E7%9A%84%E7%A9%BA%E9%97%B4%E5%88%86%E5%B8%83&variant=zh-mo
land_reference = data.coverages[6][::5, ::5]  # [6]代表用四月降水量信息来得到陆地信息（因为有情报的都是陆地），每五个挑出（减小机器负担）
land_mask = (land_reference > -9999).ravel()  # 矩阵中的缺失数据用-9999来表示(是海洋), 形成非缺失值的mask，即为陆地mask
xy = np.vstack([Y.ravel(), X.ravel()]).T
xy = np.radians(xy[land_mask])  # xy需要显示的行数被[land_mask]挑出来，度转换为弧
fig, ax = plt.subplots(1, 2)
fig.subplots_adjust(left=0.05, right=0.95, wspace=0.05)
species_names = ['Bradypus Variegatus', 'Microryzomys Minutus']
cmaps = ['Purples', 'Reds']
for i, axi in enumerate(ax):
    axi.set_title(species_names[i])
    # 画地理图
    m = Basemap(projection='cyl', llcrnrlat=Y.min(), urcrnrlat=Y.max(), llcrnrlon=X.min(), urcrnrlon=X.max(),
                resolution='c', ax=axi)
    m.drawmapboundary(fill_color='#DDEEFF')
    m.drawcoastlines()
    m.drawcountries()
    # 构建球形分布核密度估计
    kde = KernelDensity(bandwidth=0.03, metric='haversine')  # 'haversine'衡量球面距离
    kde.fit(np.radians(latlon[species == i]))  # 获取各种类的地理位置信息，化为弧度值，埋入模型
    # 计算大陆值，-9999是海洋
    Z = np.full(land_mask.shape[0], -9999.0)  # np.full()生成land_mask.shape[0]形状，-9999的数组
    Z[land_mask] = np.exp(kde.score_samples(xy))  # score_samples()返回概率密度对数值，只计算陆地的，xy是陆地弧度值坐标
    Z = Z.reshape(X.shape)  # 化为X形状供显示
    # 画出密度轮廓
    levels = np.linspace(0, Z.max(), 25)  # Z.max()是最大密度估计
    # 输入的参数是x,y对应的网格数据以及此网格对应的高度值levels，之前先要调用np.meshgrid(x,y)把x,y值转换成网格数据
    axi.contourf(X, Y, Z, levels=levels, cmap=cmaps[i])
plt.show()

核密度估计求带宽

# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.neighbors import KernelDensity
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import LeaveOneOut
sns.set()


def make_data(N, f=0.3, rseed=1):
    rand = np.random.RandomState(rseed)
    x = rand.randn(N)
    x[int(f * N):] += 5  # f * N以后全部增加5
    return x


x = make_data(20)
x_d = np.linspace(-4, 8, 1000)
# 初始化并埋入数据
kde = KernelDensity(bandwidth=1.0, kernel='gaussian')
kde.fit(x[:, None])
# score_samples 返回概率密度的对数值

logprob = kde.score_samples(x_d[:, None])
plt.fill_between(x_d, np.exp(logprob), alpha=0.5)
plt.plot(x, np.full_like(x, -0.01), '|k', markeredgewidth=1)
plt.ylim(-0.02, 0.22)

bandwidths = 10 ** np.linspace(-1, 1, 100)
grid = GridSearchCV(KernelDensity(kernel='gaussian'), {'bandwidth': bandwidths}, cv=LeaveOneOut())
grid.fit(x[:, None])
print('grid.best_params_ is: ', grid.best_params_)
plt.show()

高斯内核实现的核密度估计

# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm  # 可以实现正态分布
sns.set()


def make_data(N, f=0.3, rseed=1):
    rand = np.random.RandomState(rseed)
    x = rand.randn(N)
    x[int(f * N):] += 5  # f * N以后全部增加5
    return x


x = make_data(20)
'''
x_d = np.linspace(-4, 8, 2000)
# 只要距离在0.5以内则被计数，以此作为密度
density = sum((abs(xi - x_d) < 0.5) for xi in x)  # 计算x_d里的每一个刻度到x的距离小于0.5为真的数量
plt.fill_between(x_d, density, alpha=0.5)  # x_d对应一个density值，对着X轴填色
plt.plot(x, np.full_like(x, -0.1), '|k', markeredgewidth=1)
plt.axis([-4, 8, -0.2, 8])  # X轴范围，Y轴范围
'''
x_d = np.linspace(-4, 8, 1000)
density = sum(norm(xi).pdf(x_d) for xi in x)  # 由xi处的正态分布构成的在x_d范围内的概率密度函数
plt.fill_between(x_d, density, alpha=0.5)
plt.plot(x, np.full_like(x, -0.1), '|k', markeredgewidth=1)
plt.axis([-4, 8, -0.2, 5])
plt.show()


方块堆叠的频次直方图

# -*- coding: UTF-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()


def make_data(N, f=0.3, rseed=1):
    rand = np.random.RandomState(rseed)
    x = rand.randn(N)
    x[int(f * N):] += 5  # f * N以后全部增加5
    return x


x = make_data(1000)
hist = plt.hist(x, bins=30, density=True)
density, bins, patches = hist
print('density:\n ', density)
print('bins:\n ', bins)
print('patches:\n ', patches)
widths = bins[1:] - bins[:-1]
print('(density * widths).sum() is: ', (density * widths).sum())

x2 = make_data(20)
bins = np.linspace(-5, 10, 10)
fig, ax = plt.subplots(1, 2, figsize=(12, 4), sharex=True, sharey=True, subplot_kw={'xlim': (-4, 9), 'ylim': (-0.02, 0.3)})
fig.subplots_adjust(wspace=0.05)
for i, offset in enumerate([0.0, 0.6]):
    print('bins + offset:\n', bins + offset)
    ax[i].hist(x2, bins=bins + offset, density=True)  # 指定bins区间
    # np.full_like(): 返回与给定数组具有相同形状和类型的数组。并且数组中元素的值是fill_value的值
    ax[i].plot(x2, np.full_like(x2, -0.01), '|k', markeredgewidth=1)  # markeredgewidth：竖线条宽度; |k: 黑色竖线
    print('x2:\n', x2)

fig2, ax2 = plt.subplots()
bins = np.arange(-3, 8)
ax2.plot(x2, np.full_like(x2, -0.1), '|k', markeredgewidth=1)
for count, edge in zip(*np.histogram(x2, bins)):  # 打包把组合里各自元素赋予count和edge
    print('np.histogram(x2, bins):\n', np.histogram(x2, bins))  # 返回2个值，第一个是各个区间里的个数，第二个是区间段被刻度值隔出来的刻度值
    for i in range(count):  # 区间内有几个元素就画几个矩形
        ax2.add_patch(plt.Rectangle((edge, i), 1, 1, alpha=0.5))  # 是矩形左下角坐标，宽，高，透明度
ax2.set_xlim(-4, 8)
ax2.set_ylim(-0.2, 8)
plt.show()


GMM高斯混合模型的可视化

# -*- coding: UTF-8 -*-
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.mixture import GaussianMixture
from sklearn.datasets.samples_generator import make_blobs
from matplotlib.patches import Ellipse  # 画椭圆的类

sns.set()


def draw_ellipse(position, covariance, ax=None, **kwargs):
    # 做椭圆需要协方差和位置信息
    ax = ax or plt.gca()
    # 协方差换成主轴
    if covariance.shape == (2, 2):
        # 分解奇异值
        print('covariance:\n', covariance)
        # https://blog.csdn.net/rainpasttime/article/details/79831533?utm_source=app
        U, s, Vt = np.linalg.svd(covariance)  # compute_uv的取值是为0或者1，默认值为1，表示计算u,s,v。为0的时候只计算s
        print('s:\n', s)
        print('Vt:\n', Vt)
        # arctan2(y, x) 是该点(x, y) 对应原点形成的三角形,求反正切对应的弧度数(过原点和x轴的那个角)
        # 控制椭圆罩住的角度
        angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))  # 弧度换为角度，atan2 的用法一样（用C库所以更快）
        print('angle is：', angle)
        print('U:\n', U)
        print('U[1, 0], U[0, 0]):\n', U[1, 0], U[0, 0])
        width, height = 2 * np.sqrt(s)  # 奇异值分配出去，椭圆大小
    else:  # 若不是2*2矩阵
        angle = 0
        width, height = 2 * np.sqrt(covariance)  # 就用自己
    # 画椭圆
    for nsig in range(1, 4):  # 遍历椭圆内概率密度分层的数量
        # 绘制椭圆，第二个参数是椭圆的长直径，第三个是短直径，angle是逆时针旋转角度
        ax.add_patch(Ellipse(position, nsig * width, nsig * height, angle, **kwargs))


def plot_gmm(gmm, X, label=True, ax=None):
    ax = ax or plt.gca()
    labels = gmm.fit(X).predict(X)
    if label:
        ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2)
    else:
        ax.scatter(X[:, 0], X[:, 1], s=40, zorder=2)
    ax.axis('equal')
    w_factor = 0.2 / gmm.weights_.max()
    print('\ngmm.means_:\n', gmm.means_, '\ngmm.covariances_:\n', gmm.covariances_, '\ngmm.weights_:\n', gmm.weights_)
    for pos, covar, w in zip(gmm.means_, gmm.covariances_, gmm.weights_):  # 画出椭圆
        print('w * w_factor:', w * w_factor)
        draw_ellipse(pos, covar, alpha=w * w_factor)  # alpha通过**kwargs传入


X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)
X = X[:, ::-1]
rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))  # 叉乘投影 (400,2) X (2,2)，变成椭圆
# gmm = GaussianMixture(n_components=4).fit(X)
# gmm = GaussianMixture(n_components=4, covariance_type='full', random_state=42).fit(X)
gmm = GaussianMixture(n_components=4, random_state=42).fit(X_stretched)
labels = gmm.predict(X)
probs = gmm.predict_proba(X)
# print(probs[:5].round(3))
size = 50 * probs.max(1) ** 2
# plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=size)
plot_gmm(gmm, X_stretched)
plt.show()

用K最近邻色彩压缩

# -*- coding: UTF-8 -*-
from sklearn.datasets import load_sample_image
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import MiniBatchKMeans


def plot_pixels(data, title, colors=None, N=10000):  # 前1w个像素
    if colors is None:
        colors = data
    # 随机选择子集
    rng = np.random.RandomState(0)

    i = rng.permutation(data.shape[0])[:N]  # 随机选1万个序号
    colors = colors[i]  # 随机选1w个像素点
    # print(colors)
    R, G, B = data[i].T  # 把R，G，B的值们找出来
    fig, ax = plt.subplots(1, 2, figsize=(16, 6))
    ax[0].scatter(R, G, color=colors, marker='.')
    ax[0].set(xlabel='Red', ylabel='Green', xlim=(0, 1), ylim=(0, 1))
    ax[1].scatter(R, B, color=colors, marker='.')
    ax[1].set(xlabel='Red', ylabel='Blue', xlim=(0, 1), ylim=(0, 1))
    fig.suptitle(title, size=20)


china = load_sample_image("china.jpg")
# ax1 = plt.axes(xticks=[], yticks=[])
# ax1.imshow(china)
print('china.shape: ', china.shape)
# print('china: ', china)
data = china / 255.0  # 化为0-1区间
data = data.reshape(427 * 640, 3)  # 化成n_samplesXn_features
print('data.shape: ', data.shape)
# plot_pixels(data, title='Input color space: 16 million possible colors')  # RGB颜色空间中的像素分布
kmeans = MiniBatchKMeans(16)  # 更快的算法计算数据子集
kmeans.fit(data)
print('kmeans.predict(data).shape:', kmeans.predict(data).shape)  # 降维
# print('kmeans.predict(data):', kmeans.predict(data))  # 降维
# 降维后的kmeans.predict(data)这个列表的各个数字代表kmeans.cluster_centers_簇中心（一共16个色簇）的需要提出来拼接的行索引
new_colors = kmeans.cluster_centers_[kmeans.predict(data)]
print('kmeans.cluster_centers_.shape:', kmeans.cluster_centers_.shape)  # 簇中心，这16个代表色彩

print('new_colors.shape:', new_colors.shape)
plot_pixels(data, colors=new_colors, title="Reduced color space: 16 colors")

china_recolored = new_colors.reshape(china.shape)  # 在原来的图像空间china.shape：（427*640*3）上还原成原始尺寸
fig2, ax2 = plt.subplots(1, 2, figsize=(16, 6), subplot_kw=dict(xticks=[], yticks=[]))
fig2.subplots_adjust(wspace=0.05)
ax2[0].imshow(china)
ax2[0].set_title('Original Image', size=16)
ax2[1].imshow(china_recolored)
ax2[1].set_title('16-color Image', size=16)
plt.show()
"""
# 按照b的顺序用a的行来组成新的矩阵
a = np.mat([[1, 2, 3],
            [4, 5, 6]])
b = np.array([1, 1, 0, 0, 0, 1, 0])
c = a[b]
print('c:\n', c)
"""
通过 WordPress.com 设计一个这样的站点
从这里开始